Volume of a Combination of Solids

A hollow sphere of internal and external radii $6 \mathrm{cm} \& 8 \mathrm{cm}$ respectively, is melted and recast into small cones of base radius $2 \mathrm{cm}$ and height $8 \mathrm{cm}$. Find the number of cones.

How many lead shots each $3 \mathrm{mm}$ in diameter can be made from a cuboid of dimensions $9 \mathrm{cm}\times 11 \mathrm{cm}\times 12 \mathrm{cm}$? $($Assume $\mathrm{\pi }=\frac{22}{7})$

A $14 \mathrm{m}$ deep well with an inner diameter $10 \mathrm{m}$ is dug and the earth taken out is evenly spread all around the well to form an embankment of width $5 \mathrm{m}$. If the height of the embankment is $k \mathrm{m}$, find the value of $k$ up to two decimal places. (Take $\mathrm{\pi }=\frac{22}{7}$)

The volume of a hemisphere of radius $3 \mathrm{cm}$ is 

A solid is in the form of a cone mounted on a right circular cylinder, both having same radii as shown in the figure. The radius of the base and height of the cone are $7 \mathrm{cm}$ and $9 \mathrm{cm}$ respectively. If the total height of the solid is $30 \mathrm{cm}$, find the volume of the solid (in ${\mathrm{cm}}^3$). [Assume $\mathrm{\pi }=\frac{22}{7}$]

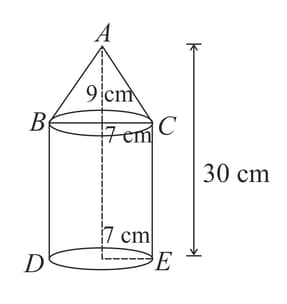
The bottom of a right cylindrical shaped vessel made from metallic sheet is closed by a cone-shaped vessel as shown in the figure. The radius of the circular base of the cylinder and radius of the circular base of the cone are each is equal to $7 \mathrm{cm}$. If the height of the cylinder is $20 \mathrm{cm}$ and height of cone is $3 \mathrm{cm}$, calculate the cost of milk (in $₹$) to fill completely this vessel at the rate of $₹20$ per litre. [Take $\mathrm{\pi }=\frac{22}{7}$]

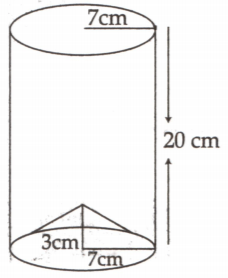
How many silver coins of diameter $5 \mathrm{cm}$ and thickness $4 \mathrm{mm}$ have to be melted to prepare a cuboid of $12 \mathrm{cm}\times 11 \mathrm{cm}\times 5 \mathrm{cm}$ dimension? Assume $\mathrm{\pi }=\frac{22}{7}$.

The volume of a cube is $1000 {\mathrm{cm}}^3$. Find its side in $\mathrm{cm}$.

In a hemispherical bowl of $2.1 \mathrm{cm}$ radius ice-cream is there. Find the volume of the bowl (in ${\mathrm{cm}}^3$), correct to three decimal places. [Assume $\mathrm{\pi }=\frac{22}{7}$]

If the side of a cube is $5 \mathrm{cm}$, then find its volume in ${\mathrm{cm}}^3$.

Volume of a right circular cone is

The volume of a cube of side $3 \mathrm{cm}$ is 

The radius of a sector is $12 \mathrm{cm}$ and angle is $120°$. By coinciding its straight sides, a cone is formed. Find the volume of that cone.

A cone of maximum height is cut from a cube of edge $14 \mathrm{cm}$. Find the volume of the cone.

The circumference of the base of a conical tent is $9 \mathrm{m}$ and height is $44 \mathrm{m}$. Find the volume of air inside it in ${\mathrm{m}}^3$.

Find the slant height of the right circular cone in $\mathrm{cm}$, whose volume is $1232 {\mathrm{cm}}^3$ and height is $24 \mathrm{cm}$.

If both ends of a hollow cylinder are open. Its height is $20 \mathrm{cm}$ and internal and external radius are $26 \mathrm{cm}$ and $30 \mathrm{cm}$ respectively. Find the volume of this hollow cylinder in ${\mathrm{cm}}^3$.

If the volume of a cylinder is $30\mathrm{\pi } {\mathrm{cm}}^3$ and area of base is $6\mathrm{\pi } {\mathrm{cm}}^2$, then find height of cylinder in $\mathrm{cm}$.

Find the volume of cylinder in ${\mathrm{cm}}^3$, whose curved surface area is $660 {\mathrm{cm}}^2$ and height is $15 \mathrm{cm}$.

The total surface area of a solid cylinder is $462 {\mathrm{cm}}^2$. Its curved surface area is one-third of its total surface area. Find the volume of the cylinder in ${\mathrm{cm}}^3$.